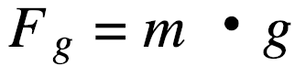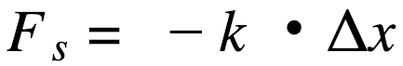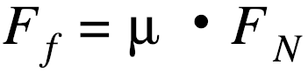Learning Targets
3.04A - I can identify the forces acting on an object/system, and draw a force diagram and/or system schema.
3.05A - I can solve force problems for basic perpendicular balanced forces.
3.05B - I can solve unbalanced force problems in the vertical direction (like elevator problems).
3.05C - I can solve problems for perpendicular forces on an object undergoing a centripetal acceleration.
3.06B - I can use equations to perform basic calculations for force problems that include motion, forces of gravity, friction, and springs. Differentiate static and kinetic friction.
3.06C - I can solve advanced problems that require concepts of motion, friction, and/or springs, requiring more than one model/equation.
3.07A - I can add vectors to find the resultant, and resolve vectors into horizontal and vertical components.
3.07B - I can solve problems when there are balanced or unbalanced forces at an angle.
3.07C - I can solve problems when there are forces acting on an incline or in a rotated system.
3.05A - I can solve force problems for basic perpendicular balanced forces.
3.05B - I can solve unbalanced force problems in the vertical direction (like elevator problems).
3.05C - I can solve problems for perpendicular forces on an object undergoing a centripetal acceleration.
3.06B - I can use equations to perform basic calculations for force problems that include motion, forces of gravity, friction, and springs. Differentiate static and kinetic friction.
3.06C - I can solve advanced problems that require concepts of motion, friction, and/or springs, requiring more than one model/equation.
3.07A - I can add vectors to find the resultant, and resolve vectors into horizontal and vertical components.
3.07B - I can solve problems when there are balanced or unbalanced forces at an angle.
3.07C - I can solve problems when there are forces acting on an incline or in a rotated system.
Can You...
- Solve various types of problems:
- Different perpendicular forces (3.05 A, B, C)
- Motion, gravity, friction, and springs (3.06 B, C)
- Forces at an angle (3.07 A, B, C)
- When analyzing the forces acting on an object...
- draw and label a force diagram for the object; (3.04A)
- if needed, break forces into components or choose a rotated coordinate system;
- find the net force on the object, the amount the forces are unbalanced;
- list knowns and unknowns for force and motion variables, use proper equations to solve.
Force Calculations
Mass vs. Weight
Mass is a measure of how much matter is in an object. We use KILOGRAMS (kg) to measure mass. This is always going to be the same, regardless of where the object is. You could think of it like counting up all the individual particles that make up an object to get an idea of how much “stuff” is in the object. In fact, it is commonly accepted that single protons and neutrons have a mass of 1.67 * 10-27 kg and an electron has a mass of 9.11 * 10-31 kg. If you counted up all the protons, neutrons, and electrons in an object, you could calculate its mass!
Weight, on the other hand, is the force of gravity acting on an object. Being a force, it is measured in Newtons (N). It depends on two things: the mass of the object and the gravitational field. Gravitational fields are strongest close to large objects such as planets. A larger, more massive planet like Jupiter has a greater gravitational field. The gravitational field on Jupiter is about 24.8 N/kg, on earth is 9.8 N/kg, on the moon is 1.62 N/kg, and far from any planets would be 0. This means you would weigh nearly 2.5 times as much on Jupiter as on earth, about 1/6th as much on the moon, and be weightless in outer space. You’ll never be massless, but you can be weightless!
Weight, on the other hand, is the force of gravity acting on an object. Being a force, it is measured in Newtons (N). It depends on two things: the mass of the object and the gravitational field. Gravitational fields are strongest close to large objects such as planets. A larger, more massive planet like Jupiter has a greater gravitational field. The gravitational field on Jupiter is about 24.8 N/kg, on earth is 9.8 N/kg, on the moon is 1.62 N/kg, and far from any planets would be 0. This means you would weigh nearly 2.5 times as much on Jupiter as on earth, about 1/6th as much on the moon, and be weightless in outer space. You’ll never be massless, but you can be weightless!
To transfer between mass and weight, use the equation above. The weight (or Fg) of an object is its mass times g. On earth, as most problems will be, the weight of an object is the force of gravity acting between the earth and the object. Again, Earth’s gravitational field is g = 9.8 N/kg. So, a 1 kg object has a weight of 9.8 N.
EXAMPLES:
What is the weight of a 3.3 kg pumpkin? Fg = 3.3 kg x 9.8 N/kg = 32.3 N
What is the mass of a 200 N weight? 200 N = m x 9.8 N/kg -> m = 200 N/9.8 N/kg = 20.4 kg
What would a 60 kg person weigh on the moon (g = 1.62 N/kg)? Fg = 60 kg x 1.62 N/kg = 97.2 N
EXAMPLES:
What is the weight of a 3.3 kg pumpkin? Fg = 3.3 kg x 9.8 N/kg = 32.3 N
What is the mass of a 200 N weight? 200 N = m x 9.8 N/kg -> m = 200 N/9.8 N/kg = 20.4 kg
What would a 60 kg person weigh on the moon (g = 1.62 N/kg)? Fg = 60 kg x 1.62 N/kg = 97.2 N
Spring Forces
This relationship between the force applied to a spring and the amount of stretch was first discovered in 1678 by English scientist Robert Hooke. As Hooke put it: Ut tensio, sic vis. Translated from Latin, this means "As the extension, so the force." In other words, the amount that the spring extends is proportional to the amount of force with which it pulls. If we had completed this study about 350 years ago (and if we knew some Latin), we would be famous! Today this quantitative relationship between force and stretch is referred to as Hooke's law and is often reported in textbooks as
where FS is the force exerted upon the spring, Δx is the amount that the spring stretches relative to its relaxed position, and k is the proportionality constant, often referred to as the spring constant.
The spring constant is a positive constant whose value is dependent upon the spring which is being studied. A stiff spring would have a high spring constant. This is to say that it would take a relatively large amount of force to cause a little displacement. The units on the spring constant are Newton/meter (N/m).
The negative sign in the above equation is an indication that the direction that the spring stretches is opposite the direction of the force which the spring exerts. For instance, when the spring was stretched below its relaxed position, Δx is downward. The spring responds to this stretching by exerting an upward force. The Δx and the F are in opposite directions. This negative sign is often ignored in calculations such that the magnitude matters not the direction.
(adapted from the Physics Classroom www.physicsclassroom.com)
EXAMPLES:
How much force is required to stretch a spring with k = 20 N/m by a distance of 4 m?
Fs = 20 N/m x 4 N/kg = 80 N (The force is opposite the direction of the stretch. We don’t know the direction of the stretch, so we only care about the magnitude of 80 N.)
If a spring stretches by 35 cm with a 4 N weight attached, what is the spring constant?
4 N = k x 0.35 m -> k = 4 N / 0.35 m = 11.4 N/m
How much would a string stretch with a spring constant of 25 N/m and a force of 87 N applied?
87 N = 25 N/m x Δx -> Δx = 87 N / 25 N/m = 3.48 m
The spring constant is a positive constant whose value is dependent upon the spring which is being studied. A stiff spring would have a high spring constant. This is to say that it would take a relatively large amount of force to cause a little displacement. The units on the spring constant are Newton/meter (N/m).
The negative sign in the above equation is an indication that the direction that the spring stretches is opposite the direction of the force which the spring exerts. For instance, when the spring was stretched below its relaxed position, Δx is downward. The spring responds to this stretching by exerting an upward force. The Δx and the F are in opposite directions. This negative sign is often ignored in calculations such that the magnitude matters not the direction.
(adapted from the Physics Classroom www.physicsclassroom.com)
EXAMPLES:
How much force is required to stretch a spring with k = 20 N/m by a distance of 4 m?
Fs = 20 N/m x 4 N/kg = 80 N (The force is opposite the direction of the stretch. We don’t know the direction of the stretch, so we only care about the magnitude of 80 N.)
If a spring stretches by 35 cm with a 4 N weight attached, what is the spring constant?
4 N = k x 0.35 m -> k = 4 N / 0.35 m = 11.4 N/m
How much would a string stretch with a spring constant of 25 N/m and a force of 87 N applied?
87 N = 25 N/m x Δx -> Δx = 87 N / 25 N/m = 3.48 m
Friction
The friction force is the force exerted by a surface as an object moves across it or makes an effort to move across it. It acts parallel to the direction of the surface in a direction to oppose the motion or attempted motion. There are two types that we will deal with: kinetic (or sliding) friction and static friction. Each depends only on the normal force between the object and surface and what is called the coefficient of friction.
Kinetic or sliding friction results when an object slides across a surface. As an example, consider pushing a box across a floor. The floor surface offers resistance to the movement of the box. We often say that the floor exerts a friction force upon the box. This is an example of a sliding friction force since it results from the sliding motion of the box.
Friction forces can also exist when the two surfaces are not sliding across each other. Static friction results between two surfaces to prevent motion when a force exists that would cause there to be motion. Suppose you were to push with 5 Newton of force on a large box to move it across the floor. The box might remain in place. A static friction force of 5 Newtons exists between the surfaces of the floor and the box balancing the force you exert to prevent the box from being set into motion. Suppose you push harder, now with 25 Newton of force and the box still doesn’t move. Static friction must now have a magnitude of 25 Newton. Then, suppose you increase the force to 26 Newton and the box finally starts to move. The box-floor surfaces could provide up to but not more than 25 Newtons of static friction force to match your applied force. Yet the two surfaces were not able to provide 26 Newton of static friction force. The amount of static friction resulting from the adhesion of any two surfaces can vary but has an upper limit. The equation is often written as:
Ff ≤ μs FN
The coefficient of friction, μ, is a positive constant that depends primarily upon the type of the surfaces that are in contact with each other. Accepted values of the coefficients of friction between common surfaces can be looked up in a table. Rougher surfaces tend to have a higher coefficient of friction. The values of μ can also provide a measure of the relative amount of adhesion or attraction of the two surfaces for each other. The more that surface molecules tend to adhere to each other, the greater the coefficient values and the greater the friction force.
Ff ≤ μs FN
The coefficient of friction, μ, is a positive constant that depends primarily upon the type of the surfaces that are in contact with each other. Accepted values of the coefficients of friction between common surfaces can be looked up in a table. Rougher surfaces tend to have a higher coefficient of friction. The values of μ can also provide a measure of the relative amount of adhesion or attraction of the two surfaces for each other. The more that surface molecules tend to adhere to each other, the greater the coefficient values and the greater the friction force.